There’s an ancient roulette scheme that’s probably about two hours older than the game itself. It’s a strategy known as the “martingale system” and was apparently popular in 18th century France, but it’s something that occurs to pretty much everyone who gives any serious thought to a mathematical gambling strategy. The method is very simple: to begin, you place a bet of a single unit on black. If you win, you pocket your winnings and place another single unit bet on black. If you lose, you double your bet. If this second bet wins, you’ve won back the original unit you lost, plus one unit of profit. If this second bet loses, you double your bet yet again. You keep on doubling your bet until you win.
This system is just fine in theory when you allow yourself infinite wealth as well as an absence of a table limit. But all roulette tables have maximum limits, typically from 2^7 to 2^10 of the minimum bet value. Which means that you’d be fine until you hit a bad stretch and lost more than seven (or ten) bets in a row. Then, of course, you’d really be up shit creek. Unfortunately, your chances of hitting that bad streak are far more likely than you’d think – which is why the system doesn’t work. For something like roulette, or coin tosses (as was chronicled in the opening sequence of Tom Stoppard’s “Rosencrantz and Guildenstern are Dead”), the system has no memory of the previous outcome. In other words, if the NFC has won the Superbowl coin toss twelve times in a row, on their thirteenth attempt their odds of winning it yet again are exactly the same as they’ve been for every other coin toss: 50%.
Gambling on the outcome of a sporting event is different. Whether it’s the point-spread or an over-under, the books take into account the previous history of a team when determining the line for a game. In terms of the point spread, if a team sucks and hasn’t covered the spread in a while, the spread gets bigger. Particularly in the case of sports gambling, where favorites tend to command a greater share of the wagers, the books will inflate the lines on bad teams for two reasons: to help limit the amount of money risked on the favorite, and to increase their chances of covering the spread and taking home a lopsided chunk of the money. And just as importantly, while every individual sportsbook will have their own minimum and maximum you’ll bump up against, a sporting event is the equivalent of a single roulette spin that takes place everywhere in town at the exact same time. So you’re free to place bets at fifty different places if you like. You’ve got a lot more freedom to keep pushing when you inevitably hit a bad streak.
It’s pretty simple logic. A simple coin toss produces a binomial distribution, a Gaussian curve. If it were true that long losing streaks in sporting events are less likely due to inflated lines (and we already do know that underdogs have a slight edge – about 1%), you’d expect that betting on an underdog would result in a curve with thinner tails than the true Gaussian distribution. On the graph the pink line represents a normal binomial distribution – where the odds are fifty percent regardless of the length of the streak. The blue line represents the distribution if the odds of winning increased with each successive loss (and decreased with each successive win). The area under the two curves is identical, but the adjusted distribution is much less likely to experience extreme winning and losing streaks due to the “memory” effect.
So how does this concept hold up in reality? Not well.
Within my own database, where I’ve got the stats from about 3,500 football games. If you bet on each team in each one of these games, for the total population you’d expect to have losing streaks of six games or worse a total of 53 times. In reality, there have been 50 such streaks during that time. Is that a significant difference? I certainly wouldn’t trust that it was.
How well does this work as a betting strategy? Also, unfortunately, not well. The graph below shows the gradual growth of your bankroll over time (including your exposure during any given week) based on a minimum bet of $10. It follows a completely predictable slope, but it’s occasionally punctuated by huge spikes downward which correspond to disastrous losing streaks. If your bankroll is substantial enough to cover these losses you’re fine, but there comes a point where you’ve been using this system for ten solid years and still manage to fall into a -$10,000 hole.
The worst losing streak was 10 consecutive losses against the spread. And which team was such a magnificent specimen of ineptitude that they managed to drop 10 straight games without covering the spread even once? One guess. You’re correct! It WAS the Oakland Raiders!
Another area where I had a look (since it’s easier to organize the statfox data and look at the results of more games) was baseball over/under values. This is where things really got blown out of the water – in one unbelievable stretch during 2008 the Florida Marlins hit the over 15 consecutive times (not including two games during that stretch which were pushes). Which means that if you were using the same $10 minimum martingale scheme I described above to bet the under, you’d reach a point where you were $640,000 in the hole with another $750,000 on the line to make it all back – for a total exposure of $1.4 million. So…this isn’t really a betting scheme I’d ever consider or endorse.
(To watch this video, right-click and hit play)
[kml_flashembed movie="http://earbuds.popdose.com/zack/Gambling/Escalator.swf" width="360" height="240" wmode="transparent" play="false" loop="false"/]
Gamblor’s season ended up being a pretty big disappointment, primarily due to Vegas’ insistence on setting short lines for all of the Green Bay games. It cost them a lot of money to do so, and it cost Gamblor a lot of money as well. The computer’s overall performance for the season was a weighted win percentage of 48.6%, for a total loss of $353. I’m not really discouraged, though, because factoring in last season’s winnings the computer now has a lifetime score of negative $71. Spread out over the last two seasons of gambling, that translates into a loss of about $3 per week, which I’d be willing to part with for the sheer entertainment value alone.
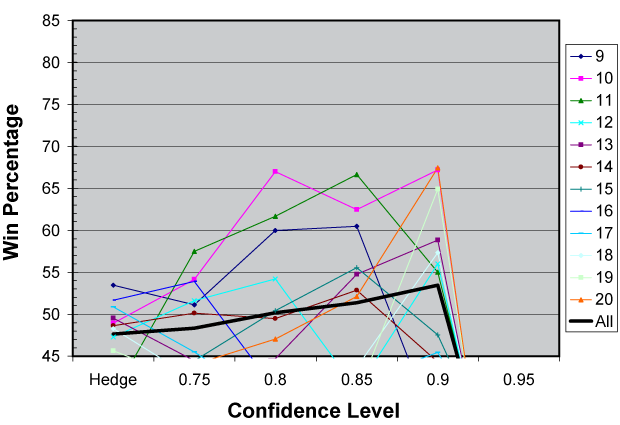
Even though it lost money this year, Gamblor actually worked the way it was supposed to. The graph below shows how it performed at increasing levels of confidence. The higher the confidence level, the better it did. The fly in the ointment was the 95% category, where the computer only selected two games (both against Green Bay) and proceeded to miss them both.
One curious thing about the 2009 season was that there were fewer flip bets this year than any other year I’ve simulated. The total number of flip bets this year was 11,300. This compares to an average (over the last 14 years) of 20,700. This meant that the computer was relying pretty heavily on hedge bets, which is where the bulk of its losses came from. The number of hedge bets was 17,700, just ten percent higher than the historical average of 15,900. Ultimately, it was a fairly quiet year for the computer, mildly disappointing but well within the bounds of my expectations.
Gamblor will be back again next year, but he’ll be joined by his spawn, Son of Gamblor. There are two major differences between the two models – Son of Gamblor accounts for the distance traveled and the time zone changes for visiting teams. Son of Gamblor also uses a weighting curve instead of Gamblor’s tiered system. I’ll explain things in detail during preseason next year. I hope the football offseason is bearable for you, and I hope you’ll join me again next year for another season of degenerate gambling.
Comments